Любая компьютерная программа представляет собой последовательность отдельных команд.
| Команда — это описание операции, которую должен выполнить компьютер. Как правило, у команды есть свой код (условное обозначение), исходные данные (операнды) и результат. |
Например, у команды "сложить два числа" операндами являются слагаемые, а результатом — их сумма. А у команды "стоп" операндов нет, а результатом является прекращение работы программы.
Результат команды вырабатывается по точно определенным для данной команды правилам, заложенным в конструкцию компьютера.
| Совокупность команд, выполняемых данным компьютером, называется системой команд этого компьютера. |
Компьютеры работают с очень высокой скоростью, составляющей миллионы - сотни миллионов операций в секунду.
Разнообразие современных компьютеров очень велико. Но их структуры основаны на общих логических принципах, позволяющих выделить в любом компьютере следующие главные устройства:
Эти устройства соединены каналами связи, по которым передается информация.
Основные устройства компьютера и связи между ними представлены на схеме (рис. 1). Жирными стрелками показаны пути и направления движения информации, а простыми стрелками — пути и направления передачи управляющих сигналов.
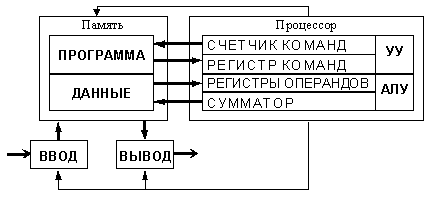
Рис.1. Общая схема компьютера
Функции памяти:
Функции процессора:
| Та часть процессора, которая выполняет команды, называется арифметико-логическим устройством (АЛУ), а другая его часть, выполняющая функции управления устройствами, называется устройством управления (УУ). |
Обычно эти два устройства выделяются чисто условно, конструктивно они не разделены.
В составе процессора имеется ряд специализированных дополнительных ячеек памяти, называемых регистрами.
| Регистр выполняет функцию кратковременного хранения числа или команды. Над содержимым некоторых регистров специальные электронные схемы могут выполнять некоторые манипуляции. Например, "вырезать" отдельные части команды для последующего их использования или выполнять определенные арифметические операции над числами. |
Основным элементом регистра является электронная схема, называемая триггером, которая способна хранить одну двоичную цифру (разряд).
| Регистр представляет собой совокупность триггеров, связанных друг с другом определённым образом общей системой управления. |
Существует несколько типов регистров, отличающихся видом выполняемых операций.
Некоторые важные регистры имеют свои названия, например:
В основу построения подавляющего большинства компьютеров положены следующие общие принципы, сформулированные в 1945 г. американским ученым Джоном фон Нейманом.

Рис.2 Джон фон Нейман, 1945 г.
1. Принцип программного управления. Из него следует, что программа состоит из набора команд, которые выполняются процессором автоматически друг за другом в определенной последовательности.
Выборка программы из памяти осуществляется с помощью счетчика команд. Этот регистр процессора последовательно увеличивает хранимый в нем адрес очередной команды на длину команды.
А так как команды программы расположены в памяти друг за другом, то тем самым организуется выборка цепочки команд из последовательно расположенных ячеек памяти.
Если же нужно после выполнения команды перейти не к следующей, а к какой-то другой, используются команды условного или безусловного переходов, которые заносят в счетчик команд номер ячейки памяти, содержащей следующую команду. Выборка команд из памяти прекращается после достижения и выполнения команды “стоп”.
Таким образом, процессор исполняет программу автоматически, без вмешательства человека.
2. Принцип однородности памяти. Программы и данные хранятся в одной и той же памяти. Поэтому компьютер не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными.
Это открывает целый ряд возможностей. Например, программа в процессе своего выполнения также может подвергаться переработке, что позволяет задавать в самой программе правила получения некоторых ее частей (так в программе организуется выполнение циклов и подпрограмм).
Более того, команды одной программы могут быть получены как результаты исполнения другой программы. На этом принципе основаны методы трансляции — перевода текста программы с языка программирования высокого уровня на язык конкретной машины.
3. Принцип адресности. Структурно основная память состоит из перенумерованных ячеек; процессору в произвольный момент времени доступна любая ячейка.
Отсюда следует возможность давать имена областям памяти, так, чтобы к запомненным в них значениям можно было впоследствии обращаться или менять их в процессе выполнения программ с использованием присвоенных имен.
Компьютеры, построенные на этих принципах, относятся к типу фон-неймановских.
Но существуют компьютеры, принципиально отличающиеся от фон-неймановских. Для них, например, может не выполняться принцип программного управления, т.е. они могут работать без “счетчика команд”, указывающего текущую выполняемую команду программы. Для обращения к какой-либо переменной, хранящейся в памяти, этим компьютерам не обязательно давать ей имя. Такие компьютеры называются не-фон-неймановскими.
Вернемся к понятию команды и проследим их выполнение в компьютере.
| Команда — это описание элементарной операции, которую должен выполнить компьютер. |
В общем случае, команда содержит следующую информацию:
В зависимости от количества операндов, команды бывают:
Команды хранятся в ячейках памяти в двоичном коде.
В современных компьютерах длина команд переменная (обычно от двух до четырех байтов), а способы указания адресов переменных весьма разнообразные.
В адресной части команды может быть указан, например:
Рассмотрим несколько возможных вариантов команды сложения (англ. add — сложение), при этом вместо цифровых кодов и адресов будем пользоваться условными обозначениями:
| add | x |
| add | x | y |
| add | x | y | z |
Выполнение команды можно проследить по рис.1:
Как пpавило, этот процесс разбивается на следующие этапы:
Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
Данные и команды в памяти компьютера и в регистрах процессора представляются в виде двоичных последовательностей различной структуры и длины.
Существуют различные физические способы кодирования двоичной информации, но
чаще всего единица кодируется более высоким уровнем напряжения, чем ноль
(или наоборот), например:
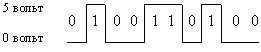
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений.
Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис.3. Таблица истинности — в таблице 1.
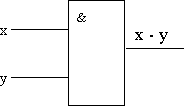
рис.3
| x | y | xЧy |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = xЧy (читается как "x и y").
Операция конъюнкции на функциональных схемах обозначается знаком “&” (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений.
Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение схемы ИЛИ представлено на рис.4. Знак “1” на схеме — от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y"). Таблица истинности — в табл.2.
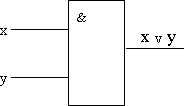
Рис.
4
| x | y | x v y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом
x этой схемы и выходом z можно записать соотношением z =
![]() , где
, где ![]() читается
как "не x" или "инверсия х".
читается
как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение инвертора — на рисунке 5, а таблица истинности — в табл. 3.
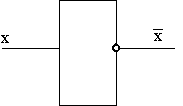
Рис.
5
| x | |
| 0 | 1 |
| 1 | 0 |
С х е м а И - НЕ
Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И.
Связь между выходом z и входами x и y схемы записывают
следующим образом: ![]() , где
, где ![]() читается как "инверсия x и y".
читается как "инверсия x и y".
Условное обозначение схемы И-НЕ представлено на рисунке 6. Таблица истинности схемы И-НЕ — в табл.4.
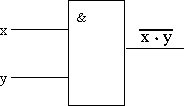
Рис.
6
| x | y | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
С х е м а ИЛИ - НЕ
Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.
Связь между выходом z и входами x и y схемы записывают
следующим образом: ![]() , где
, где ![]() , читается как "инверсия x или y". Условное
обозначение схемы ИЛИ-НЕ представлено на рис.7.
, читается как "инверсия x или y". Условное
обозначение схемы ИЛИ-НЕ представлено на рис.7.
Таблица истинности схемы ИЛИ-НЕ — в табл.5.
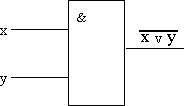
Рис.
7
| x | y | |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. |
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рис.8.

Рис.
8
Он имеет два симметричных входа S и R и два симметричных выхода Q и ![]() , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала ![]() .
.
На каждый из двух входов S и R могут подаваться входные сигналы в виде
кратковременных импульсов ( ![]() ).
).
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.
На рис.9 показана реализация триггера с помощью вентилей ИЛИ-НЕ и соответствующая таблица истинности.
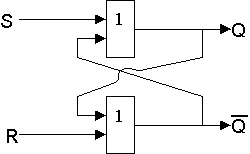
Рис.
9
| S | R | Q | |
| 0 | 0 | запрещено | |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | хранение бита | |
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ-НЕ (табл. 5.5).
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 • 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
| Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел. |
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров, с рассмотрения которых мы и начнём. Условное обозначение одноразрядного сумматора на рис.10.
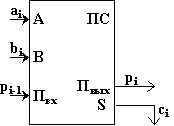
Рис.
10
При сложении чисел A и B в одном i-ом разряде приходится иметь дело с тремя цифрами:
1. цифра ai первого слагаемого;
2. цифра bi второго слагаемого;
3. перенос pi–1 из младшего разряда.
В результате сложения получаются две цифры:
1. цифра ci для суммы;
2. перенос pi из данного разряда в старший.
Таким образом, одноразрядный двоичный сумматор есть устройство с тремя входами и двумя выходами, работа которого может быть описана следующей таблицей истинности:
| Входы | Выходы | |||
| Первое слагаемое | Второе слагаемое | Перенос | Сумма | Перенос |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
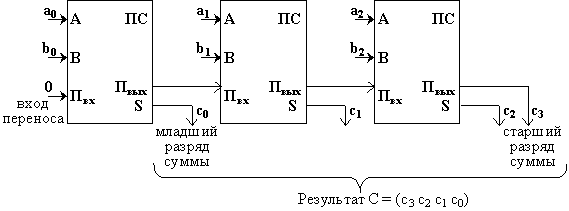
Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Например, схема вычисления суммы C = (с3 c2 c1 c0) двух двоичных трехразрядных чисел A = (a2 a1 a0) и B = (b2 b1 b0) может иметь вид: